EM properties

Свет как электромагнитная волна

Спектр электромагнитного излучения

Волновая природа света

В рамках волновой теории свет представляет собой электромагнитные волны. Под светом в настоящее время понимают электромагнитное излучение оптического диапазона, включающего видимое, инфракрасное (ИК) и ультрафиолетовое (УФ) излучение. Границы оптического диапазона, а также границы между его участками установлены на основе экспериментальных данных и не являются абсолютно точными. Диапазон видимых длин волн: 380 нм \(\leqslant \lambda\leqslant \) 760 нм, частота колебаний порядка \( \nu \sim 10^{15} \) Гц, период колебаний \( T \sim 10^{-15} \) с (фемтосекунды).

Электромагнитная волна – колебания напряженности электрического и магнитного полей, распространяющиеся в пространстве с конечной скоростью.

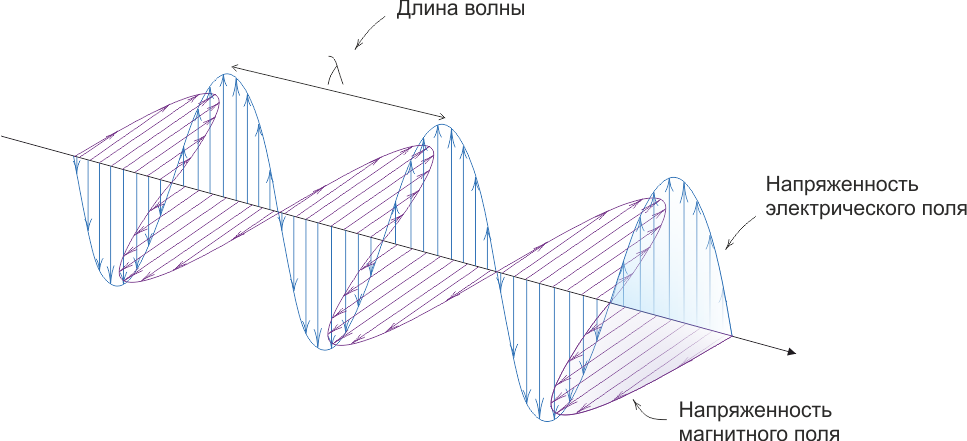
Плоская электромагнитная волна

Математическое описание оптических явлений строится на основе базовых уравнений электромагнетизма – уравнениях Максвелла. Из уравнений Максвелла следует
1) факт существования электромагнитных волн,
2) распространение электромагнитных волн в вакууме с конечной скоростью,

\begin{equation} c = \frac{1}{\sqrt{\varepsilon_0 \mu_0}} \end{equation}

\( c = \frac{1}{\sqrt{\varepsilon_0 \mu_0}} \)

3) распространение электромагнитных волн в однородной изотропной среде со скоростью

\begin{equation} v = \frac{c}{n}, n=\sqrt{\varepsilon \mu}, \mu=1, n=\sqrt{\varepsilon} \end{equation}

\(v = \frac{c}{n}, n=\sqrt{\varepsilon \mu},\) \( \mu=1, n=\sqrt{\varepsilon}\)

4) Частные решения в виде плоской и сферической волн.

Плоская монохроматическая волна

Напряженность электрического поля такой волны описывается выражением:

\begin{equation} \vec{E}(\vec{r},t)=\vec{E}_0 \cos (\omega t -kz +\phi_0) \end{equation}

\( \vec{E}(\vec{r},t)=\vec{E}_0 \cos (\omega t -kz +\phi_0) \)

– волна распространяется вдоль оси z,

\begin{equation} \vec{E}(\vec{r},t)=\vec{E}_0 \cos (\omega t -k\vec{n}\vec{r} +\phi_0) \end{equation}

\( \vec{E}(\vec{r},t)=\vec{E}_0 \cos (\omega t -k\vec{n}\vec{r} +\phi_0) \)

– волна распространяется в направлении, задаваемом вектором \( \vec{k} \). Здесь \( \vec{k} = k \vec{n} =\frac{2 \pi}{\lambda} \vec{n}\) – волновой вектор, длина которого равна волновому числу, а направление совпадает с направлением распространения волны (т.е. с нормалью к волновому фронту). В комплексном виде

\begin{equation} \vec{E}(z,t)=\vec{E}_0 \exp [i(\omega t -kz +\phi_0)] \end{equation}

\( \vec{E}(z,t)=\vec{E}_0 \exp [i(\omega t -kz +\phi_0)] \)

Параметры плоской монохроматической волны

\( \vec{E}_0 \) – амплитуда волны, в общем случае, комплексная.
\( (\omega t -kz +\phi_0)\) — фаза волны,
\( \phi_0 \) – начальная фаза волны,
\( \omega \) – циклическая частота волны, \( \omega = 2 \pi \nu \) , где \( \nu \) — частота волны (Гц),
\( \nu = \frac{1}{T} \) , где \( T \) – период волны,
\(\vec{k} = k \vec{n} =\frac{2 \pi}{\lambda} \vec{n}\) – волновой вектор, направлен в направлении распространения вол-ны (в частном случае – вдоль оси z), перпендикулярно к волновой поверхности (поверхности равных фаз). \( k = |\vec{k}| \) — волновое число, \( k =\frac{2 \pi}{\lambda} \),
\( \lambda = v T \) — длина волны или ее пространственный период, \(v\) – фазовая ско-рость волны (скорость распространения волнового фронта волны) , \( kz= \frac{2 \pi}{\lambda} z = \frac{2 \pi}{ v T}z = \frac{2 \pi n}{ c T}z = \frac{2 \pi n}{ \lambda_0}z = \frac{2 \pi}{ v T}\Delta\) где \(n\) - показатель преломления среды, \(\lambda_0\) - длина волны в вакууме,
величина \(\Delta\), равная произведению показателя преломления на геометриче-скую длину пути \(\Delta=n z\), называется оптической длиной пути.

Свойства плоской монохроматической волны

1. Волна монохроматическая – колебания напряженностей электрического и магнитного полей происходят на одной частоте, т.е гармонические (по закону sin, cos).
2. Волна плоская – волновая поверхность (поверхность равных фаз, или поверхность постоянной фазы) – плоскость, т.е. удовлетворяет уравнению плоскости: z=const (в общем случае \( \vec{k}\vec{r} = const\)). Волновой фронт – это волновая поверхность на границе между возмущенной и невозмущенной частью пространства.

Плоская электромагнитная волна

Сферическая электромагнитная волна

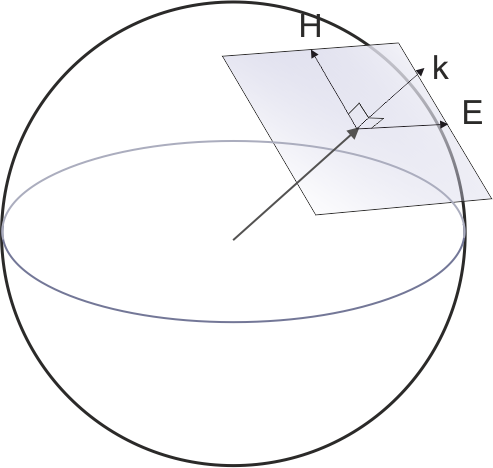
3. Поперечность электромагнитной волны – колебания векторов \(\vec{E} \) и \(\vec{H} \) перпендикулярны направлению распространения волны \(\vec{k} \);
4. Правая тройка векторов – векторы \(\vec{E} \), \(\vec{H} \), \(\vec{k} \) образуют правую ортогоналъную тройку векторов;
5. Связь между векторами \(\vec{E} \) и \(\vec{H} \) – синфазность колебаний этих векторов;
6. Связь между амплитудами векторов \(\vec{E} \) и \(\vec{H} \):

\begin{equation} E_0=\sqrt{\frac{\mu \mu_0}{\varepsilon \varepsilon_0}} H_0 \end{equation}

\( E_0=\sqrt{\frac{\mu \mu_0}{\varepsilon \varepsilon_0}} H_0 \)

7. Поляризация электромагнитной волны.
Поляризация – свойство света, обусловленное поперечностью электромагнитных волн. Поляризация характеризует структуру колебаний вектора напряженности электрического поля в плоскости, перпендикулярной направлению распространения волны. Конец вектора \(\vec{E} \) в этой плоскости может описывать различные фигуры (линию, эллипс, круг). Если с течением времени эти фигуры не изменяются, свет полностью поляризован (линейно, эллиптически, циркулярно). Если состояния поляризации (фигуры) с течением времени изменяются случайным образом, свет не поляризован;

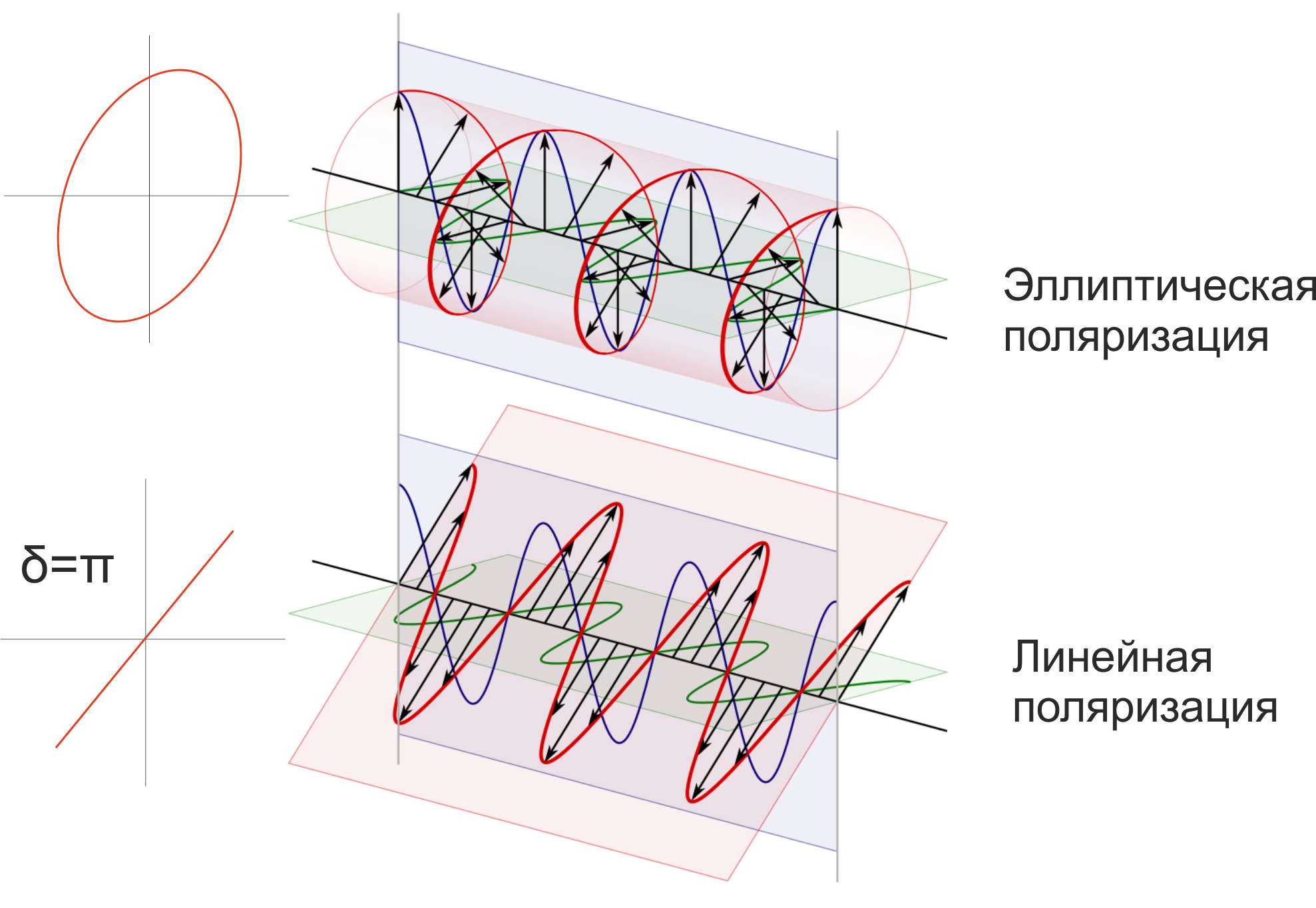
Плоская электромагнитная волна: линейная и эллиптическая поляризации

8. Интенсивность плоской монохроматической волны пропорциональна квадрату ее амплитуды;

\begin{equation} I \sim |E|^2 \end{equation}

\( I \sim |E|^2 \)

9. Связь между волной и лучом. Световые лучи – это нормали к волновой поверхности (поверхности постоянной фазы волны).

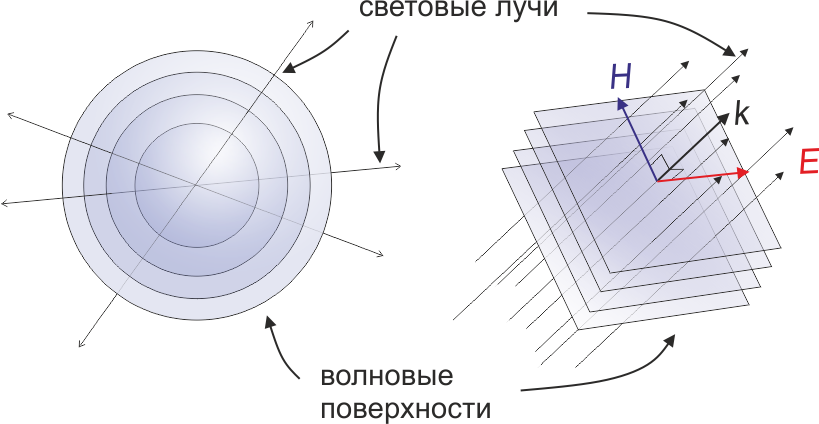
Сферическая и плоская электромагнитные волны

10. Почему для описания светового поля используется вектор \(\vec{E} \), а не \(\vec{H} \)?
Выражение интенсивности света через вектор \(\vec{E} \) , а не \(\vec{H} \), имеет физический смысл. Сравним действие электрического и магнитного полей на заряд q, опреде-ляемого силами Лоренца: силой электрического поля \(\vec{F}_{el} = q \vec{E}\) и магнитного поля – \(\vec{F}_{mag} = q [\vec{v}_q,\vec{B}]\) , где \(\vec{v}_q\) - скорость движения заряда, а \(\vec{B}\) вектор индукции магнитного поля.

\begin{equation} \frac{F_{el}}{F_{mag}} = \frac{q E}{q v_q B \sin{\pi/2}} = = \frac{E}{v_q \mu \mu_0 H} = \frac{1}{v_q}\sqrt{\frac{1}{\mu \mu_0 \varepsilon \varepsilon_0}} \\ \frac{1}{v_q}\sqrt{\frac{1}{\mu \mu_0 \varepsilon \varepsilon_0}} = \frac{1}{v_q \sqrt{\mu \mu_0} \sqrt{\varepsilon \varepsilon_0}} = =\frac{1}{v_q \sqrt{\varepsilon_0 \mu_0} \sqrt{\varepsilon \mu}}=\frac{c}{v_q n}=\frac{v}{v_q}\sim 10^4 \end{equation}

\( \frac{F_{el}}{F_{mag}} = \frac{q E}{q v_q B \sin{\pi/2}} = \)
\( = \frac{E}{v_q \mu \mu_0 H} = \frac{1}{v_q}\sqrt{\frac{1}{\mu \mu_0 \varepsilon \varepsilon_0}} \)
\( \frac{1}{v_q}\sqrt{\frac{1}{\mu \mu_0 \varepsilon \varepsilon_0}} = \frac{1}{v_q \sqrt{\mu \mu_0} \sqrt{\varepsilon \varepsilon_0}} \)
\(=\frac{1}{v_q \sqrt{\varepsilon_0 \mu_0} \sqrt{\varepsilon \mu}}=\frac{c}{v_q n}=\frac{v}{v_q}\sim 10^4\)

где \(v\) - фазовая скорость волны.

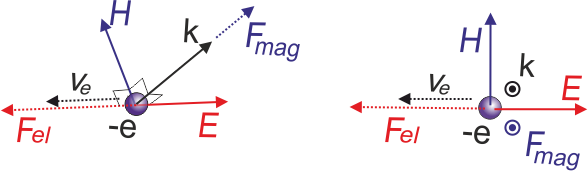
Силы, действующие на электрон в поле электромагнитной волны

Сферическая волна

Напряженность электрического поля сферической волны описывается выражением:

\begin{equation} \vec{E}(r,t)=\frac{\vec{E}_0}{r}\cos{(wt-kr+\varphi_0)} \end{equation}

\( \vec{E}(r,t)=\frac{\vec{E}_0}{r}\cos{(wt-kr+\varphi_0)} \)

Это выражение записано в сферической системе координат. Оно описывает сферическую волну, расходящуюся от точечного источника, расположенного в начале координат. Волновые поверхности сферической волны представляют собой сферы. В отличие от плоской волны, амплитуда сферической волны не является постоянной, а убывает с расстоянием.